This class can perform a one dimensional bin packing. It could be used to: Sort packages of a certain weight into containers that can carry a given weight, cut 2x4s of a certain length into the required pieces with minimal waste, fill disks with a list of files… An example of a two dimensional bin packing is fitting images onto a page and a 3D example is fitting packages into a truck. A mix between standard Best Fit and Worst Fit algorithms is used. Data must be entered and sorted descending before calling the main PackBins Sub.
Time Complexity (TC) of this function where
N = # of items B = min # of bins needed = 1 + int(sum(1 to N) of itemsize / BinCapacity) TC = N * B (i.e. we loop through the N items comparing most of them to each bin)On my computer: 1000items-> ~200bins ==> 200,000 .06sec 5000items->~1000bins ==> 5,000,000 1.50sec
If the average size of an item is 1/2 bin size then TC = N * N/2 or more generally:
TC = N * N * Save%
TC = N 2 * Save%
(where S is the percentage of average item size relative to bin capacity)
So if average item size doesn’t change doubling the number of items quadruples time spent. Using the second test time above would mean 5 million items would take a whopping 17.4 days to sort (5mil/5000 → 10002 * 1.5sec). However, we could assume that not much is gained by considering all items together. You could instead break it down to 5000 reps of the 1000 item problem which would give 0.06s * 5000 = 5min. You might save the results of each repetition, but remove the items in the last bin if not near full and return them to the items remaining to be sorted.
Also note that as S is decreased the number of bins needed will approach the optimum. And as S is increased the assumption above is less true; it becomes more important to check as many items as possible to reduce the number of bins needed. I lack the math skills to prove it, but it’s not difficult to see that if you have 1000 items with values ranging from 0 to 1000 and the bin capacity is 1000, there will be many bins with a large first item that won’t have a near perfect match which will result in extra bins needed. So given a maximum item size Smax there should be a point at which checking more items causes a huge time penalty without doing much to optimize the number of bins needed: Iopt = Smax * M (where if Save% is large M > 1).
One last note: It is perfectly possible that the number of bins needed far exceeds the predicted optimum without implying that the sort did a bad job. Consider a problem where bin capacity is 10 and you have 10 items of size 6. Total size divided by bin capacity (60/10) predicts that at least 6 bins will be needed while it is clear that 10 bins are needed.
source code with a test app (11KB).
Main function of class module
Public Sub PackBins()
Dim i As Long, j As Long, tot As Long
Dim iBestBin As Long, iWorstBin As Long, qBestBin As Long, qWorstBin As Long, x As Long
Dim iSize As Long '=m_Items(i).Size
Dim prevUbound As Long
pTightenPackageList
If UBound(m_Items) = 0 Then '1 item
ReDim m_Bins(m_iUItem To m_iUItem) 'so BinsNeeded will give correct val
Exit Function
End If
If m_BinReasonablyFull = 0 Then m_BinReasonablyFull = 0.95 * m_BinCapacity
For i = 0 To UBound(m_Items)
If m_Items(i).size <= m_BinCapacity Then tot = tot + m_Items(i).size
Next
'start with one less than min bins necessary to hold all items
'when remainder of tot / m_BinCapacity < 0.5
ReDim m_Bins(Int(tot / m_BinCapacity) + CLng((tot Mod m_BinCapacity) < m_BinCapacity / 2))
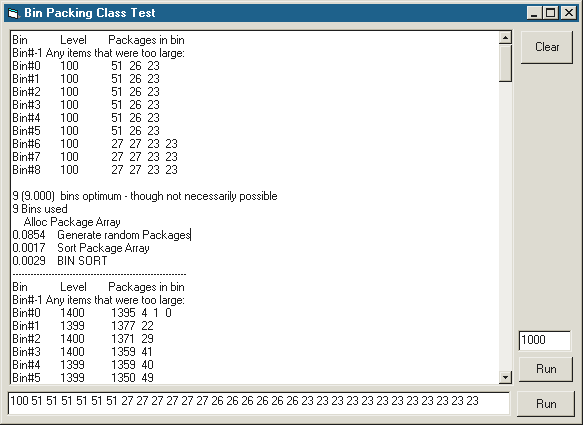
Debug.Print FormatNumber(tot / m_BinCapacity, 3) & "(i.e. " & Int(tot / m_BinCapacity) + IIf(tot Mod m_BinCapacity, 1, 0) & ") bins optimum - though not necessarily possible"
'place all items over 1/2 capacity in their own bin
qBestBin = Int(m_BinCapacity / 2)
For i = 0 To UBound(m_Items)
iSize = m_Items(i).size
If iSize > qBestBin Then
If iSize <= m_BinCapacity Then
m_Items(i).lBin = i
If i > UBound(m_Bins) Then pNewBin
m_Bins(i) = iSize 'mark bin usage
Else
m_Items(i).lBin = -1 'oversized
End If
Else
Exit For ' <= 1/2 bin capacity
End If
Next
'place the rest of the items
For i = i To UBound(m_Items)
'loop until a bin has been found
m_Items(i).lBin = -1 'no bin chosen yet
iBestBin = -1 'best bin index and flag that best bin found
iWorstBin = -1 'worst bin index and flag that fits in bin
qBestBin = m_BinReasonablyFull - 1 'a best bin has to be > this
qWorstBin = m_BinCapacity + 1
iSize = m_Items(i).size
j = 0 'current bin to check
Do
x = m_Bins(j) + iSize
'if fits in bin
If x <= m_BinCapacity Then
'is it most full bin
If x > qBestBin Then 'NOW qBestBin always= m_BinReasonablyFull-1
m_Items(i).lBin = j
m_Bins(j) = x ' m_Bins(j) + iSize
Exit Do
End If
'is it least full bin
If x < qWorstBin Then
qWorstBin = x
iWorstBin = j
End If
End If
'if current bin is empty or last bin and don't need new one it's time to decide where to place item
If (m_Bins(j) = 0) Or (j = UBound(m_Bins)) Then
If iWorstBin >= 0 Then
m_Items(i).lBin = iWorstBin
m_Bins(iWorstBin) = m_Bins(iWorstBin) + iSize
Exit Do
Else 'didn't fit - place in the empty bin or in new bin
If m_Bins(j) <> 0 Then
'we need a new bin (rare since we start with min bins
pNewBin
j = j + 1
End If
m_Items(i).lBin = j
m_Bins(j) = m_Bins(j) + iSize
Exit Do
End If
End If
'try next bin
j = j + 1
Loop 'While m_Items(i).lBin = -1 'now exit do takes care 15%faster in IDE
Next
'--------------------------------------------------------------
If m_Bins(UBound(m_Bins)) = 0 And UBound(m_Bins) > 0 Then
ReDim Preserve m_Bins(UBound(m_Bins) - 1)
End If
'try and place last items as 1st fit
'keep last bin as empty as possible
x = 0 ': j = 0
i = 0
Do 'For i = 0 To UBound(m_Items)
If m_Items(i).lBin = UBound(m_Bins) Then
If x Then
iSize = m_Items(i).size
For j = 0 To UBound(m_Bins) - 1
If m_Bins(j) + iSize <= m_BinCapacity Then
m_Bins(j) = m_Bins(j) + iSize
m_Bins(UBound(m_Bins)) = m_Bins(UBound(m_Bins)) - iSize
m_Items(i).lBin = j
Debug.Print "moved an item out of last bin"
'leave if only the first item remains in last bin
If m_Bins(UBound(m_Bins)) = x Then Exit Do
Exit For
End If
Next
Else
x = m_Items(i).size 'flag that we found and skipped first (largest) item in last bin
End If
End If
i = i + 1
Loop While i <= UBound(m_Items) 'Next
' SortPackagesByBin 'let user call this so we can see how binsort was executed
Debug.Print
End Sub
'in it's own module (this is one of the areas of .net that may differ from vb6 where this code had to be in a separate .bas module
'in .net it may be possible to simply include this structure in the class module
Option Strict Off
Option Explicit On
Module modCBinPackage
Public Structure tPackage
Dim size As Integer
Dim lBin As Integer 'bin where it has been placed
Dim name As String 'optional for caller's use (e.g. filename)
End Structure
End Module
'within CBinPack Class module (The main Sub that performs the binpacking. Other quick sort routines,
'properties and methods not shown which are in the download)
Private m_Items() As tPackage 'New cBinPackage
Private m_Bins() As Integer 'used space
Private m_BinCapacity As Integer
Private m_BinReasonablyFull As Integer 'threshold that tells whether to use BestFit or WorstFit
Private m_iUItem As Integer 'when adding packages array may be larger than necessary
'this keeps track of the last item before BinPacking
'array is shrunk so that ubound is valid
Public Sub PackBins()
Dim j, i, tot As Integer
Dim qWorstBin, iWorstBin, iBestBin, qBestBin, x As Integer
Dim iSize As Integer '=m_Items(i).Size
Dim prevUbound As Integer
pTightenPackageList()
If UBound(m_Items) = 0 Then '1 item
ReDim m_Bins(m_iUItem) 'so BinsNeeded will give correct val
Exit Sub
End If
If m_BinReasonablyFull = 0 Then m_BinReasonablyFull = 0.95 * m_BinCapacity
For i = 0 To UBound(m_Items)
If m_Items(i).size <= m_BinCapacity Then tot = tot + m_Items(i).size
Next
'start with one less than min bins necessary to hold all items
'when remainder of tot / m_BinCapacity < 0.5
ReDim m_Bins(Int(tot / m_BinCapacity) + CInt((tot Mod m_BinCapacity) < m_BinCapacity / 2))
'place all items over 1/2 capacity in their own bin
qBestBin = Int(m_BinCapacity / 2)
For i = 0 To UBound(m_Items)
iSize = m_Items(i).size
If iSize > qBestBin Then
If iSize <= m_BinCapacity Then
m_Items(i).lBin = i
If i > UBound(m_Bins) Then pNewBin()
m_Bins(i) = iSize 'mark bin usage
Else
m_Items(i).lBin = -1 'oversized
End If
Else
Exit For ' <= 1/2 bin capacity
End If
Next
'place the rest of the items
For i = i To UBound(m_Items)
'loop until a bin has been found
m_Items(i).lBin = -1 'no bin chosen yet
' If m_Items(i).size <= m_BinCapacity Then NOT NEEDED NOW THAT WE PREPLACE LARGE ITEMS
iBestBin = -1 'best bin index and flag that best bin found
iWorstBin = -1 'worst bin index and flag that fits in bin
qBestBin = m_BinReasonablyFull - 1 'a best bin has to be > this
qWorstBin = m_BinCapacity + 1
iSize = m_Items(i).size
j = 0 'current bin to check
Do
x = m_Bins(j) + iSize
'if fits in bin
If x <= m_BinCapacity Then
'is it most full bin
If x > qBestBin Then 'NOW qBestBin always= m_BinReasonablyFull-1
'This saves 10% time and produced no difference in bins needed
'for 600,000 reps with 100 random items
' If x = m_BinCapacity Then 'no need to check for better fit
'this is actually very common for small items when
'dealing with thousands of items
m_Items(i).lBin = j
m_Bins(j) = x ' m_Bins(j) + iSize
Exit Do
End If
'is it least full bin
If x < qWorstBin Then
qWorstBin = x
iWorstBin = j
End If
End If
'if current bin is empty or last bin and don't need new one it's time to decide where to place item
If (m_Bins(j) = 0) Or (j = UBound(m_Bins)) Then
If iWorstBin >= 0 Then
m_Items(i).lBin = iWorstBin
m_Bins(iWorstBin) = m_Bins(iWorstBin) + iSize
Exit Do
Else 'didn't fit - place in the empty bin or in new bin
If m_Bins(j) <> 0 Then
'we need a new bin (rare since we start with min bins
pNewBin()
j = j + 1
End If
m_Items(i).lBin = j
m_Bins(j) = m_Bins(j) + iSize
Exit Do
End If
End If
'try next bin
j = j + 1
Loop 'While m_Items(i).lBin = -1 'now exit do takes care 15%faster in IDE
' End If 'oversized package test
Next
'--------------------------------------------------------------
If m_Bins(UBound(m_Bins)) = 0 And UBound(m_Bins) > 0 Then
ReDim Preserve m_Bins(UBound(m_Bins) - 1)
End If
'try and place last items as 1st fit
'keep last bin as empty as possible
x = 0 ': j = 0
i = 0
Do 'For i = 0 To UBound(m_Items)
If m_Items(i).lBin = UBound(m_Bins) Then
If x Then
iSize = m_Items(i).size
For j = 0 To UBound(m_Bins) - 1
If m_Bins(j) + iSize <= m_BinCapacity Then
m_Bins(j) = m_Bins(j) + iSize
m_Bins(UBound(m_Bins)) = m_Bins(UBound(m_Bins)) - iSize
m_Items(i).lBin = j
Debug.Print("moved an item out of last bin")
'leave if only the first item remains in last bin
If m_Bins(UBound(m_Bins)) = x Then Exit Do
Exit For
End If
Next
Else
x = m_Items(i).size 'flag that we found and skipped first (largest) item in last bin
End If
End If
' If j = UBound(m_Bins) Then Exit For
i = i + 1
Loop While i <= UBound(m_Items) 'Next
' SortPackagesByBin 'let user call this so we can see how binsort was executed
Debug.Print("")
End Sub
//This is automatically trnaslated from VB code and probably needs editing to work
//translated using www.tangiblesoftwaresolutions.com
using System;
//Translated to VB.net. There may be some improvements to the code but this is working.
//in it's own module (this is one of the areas of .net that may differ from vb6 where this code had to be in a separate .bas module
//in .net it may be possible to simply include this structure in the class module
internal static class modCBinPackage
{
public struct tPackage
{
public int size;
public int lBin; //bin where it has been placed
public string name; //optional for caller's use (e.g. filename)
}
}
//within CBinPack Class module (The main Sub that performs the binpacking. Other quick sort routines,
//properties and methods not shown which are in the download)
private modCBinPackage.tPackage[] m_Items; //New cBinPackage
private int[] m_Bins; //used space
private int m_BinCapacity;
private int m_BinReasonablyFull; //threshold that tells whether to use BestFit or WorstFit
private int m_iUItem; //when adding packages array may be larger than necessary
//this keeps track of the last item before BinPacking
//array is shrunk so that ubound is valid
public void PackBins()
{
int j = 0;
int i = 0;
int tot = 0;
int qWorstBin = 0;
int iWorstBin = 0;
int iBestBin = 0;
int qBestBin = 0;
int x = 0;
int iSize = 0; //=m_Items(i).Size
int prevUbound = 0;
pTightenPackageList();
if (m_Items.GetUpperBound(0) == 0) //1 item
{
m_Bins = new int[m_iUItem + 1]; //so BinsNeeded will give correct val
return;
}
if (m_BinReasonablyFull == 0)
{
m_BinReasonablyFull = Convert.ToInt32(0.95 * m_BinCapacity);
}
for (i = 0; i <= m_Items.GetUpperBound(0); i++)
{
if (m_Items[i].size <= m_BinCapacity)
{
tot = tot + m_Items[i].size;
}
}
//start with one less than min bins necessary to hold all items
//when remainder of tot / m_BinCapacity < 0.5
m_Bins = new int[(Convert.ToInt32(Math.Floor((double)(tot / (double)m_BinCapacity))) + Convert.ToInt32((tot % m_BinCapacity) < m_BinCapacity / 2.0)) + 1];
//place all items over 1/2 capacity in their own bin
qBestBin = Convert.ToInt32(Math.Floor((double)(m_BinCapacity / 2.0)));
for (i = 0; i <= m_Items.GetUpperBound(0); i++)
{
iSize = m_Items[i].size;
if (iSize > qBestBin)
{
if (iSize <= m_BinCapacity)
{
m_Items[i].lBin = i;
if (i > m_Bins.GetUpperBound(0))
{
pNewBin();
}
m_Bins[i] = iSize; //mark bin usage
}
else
{
m_Items[i].lBin = -1; //oversized
}
}
else
{
break; // <= 1/2 bin capacity
}
}
//place the rest of the items
for (i = i; i <= m_Items.GetUpperBound(0); i++)
{
//loop until a bin has been found
m_Items[i].lBin = -1; //no bin chosen yet
// If m_Items(i).size <= m_BinCapacity Then NOT NEEDED NOW THAT WE PREPLACE LARGE ITEMS
iBestBin = -1; //best bin index and flag that best bin found
iWorstBin = -1; //worst bin index and flag that fits in bin
qBestBin = m_BinReasonablyFull - 1; //a best bin has to be > this
qWorstBin = m_BinCapacity + 1;
iSize = m_Items[i].size;
j = 0; //current bin to check
do
{
x = m_Bins[j] + iSize;
//if fits in bin
if (x <= m_BinCapacity)
{
//is it most full bin
if (x > qBestBin) //NOW qBestBin always= m_BinReasonablyFull-1
{
//This saves 10% time and produced no difference in bins needed
//for 600,000 reps with 100 random items
// If x = m_BinCapacity Then 'no need to check for better fit
//this is actually very common for small items when
//dealing with thousands of items
m_Items[i].lBin = j;
m_Bins[j] = x; // m_Bins(j) + iSize
break;
}
//is it least full bin
if (x < qWorstBin)
{
qWorstBin = x;
iWorstBin = j;
}
}
//if current bin is empty or last bin and don't need new one it's time to decide where to place item
if ((m_Bins[j] == 0) || (j == m_Bins.GetUpperBound(0)))
{
if (iWorstBin >= 0)
{
m_Items[i].lBin = iWorstBin;
m_Bins[iWorstBin] = m_Bins[iWorstBin] + iSize;
break;
}
else //didn't fit - place in the empty bin or in new bin
{
if (m_Bins[j] != 0)
{
//we need a new bin (rare since we start with min bins
pNewBin();
j = j + 1;
}
m_Items[i].lBin = j;
m_Bins[j] = m_Bins[j] + iSize;
break;
}
}
//try next bin
j = j + 1;
} while (true); //While m_Items(i).lBin = -1 'now exit do takes care 15%faster in IDE
// End If 'oversized package test
}
//--------------------------------------------------------------
if (m_Bins[m_Bins.GetUpperBound(0)] == 0 && m_Bins.GetUpperBound(0) > 0)
{
Array.Resize(ref m_Bins, m_Bins.GetUpperBound(0));
}
//try and place last items as 1st fit
//keep last bin as empty as possible
x = 0; //: j = 0
i = 0;
do //For i = 0 To UBound(m_Items)
{
if (m_Items[i].lBin == m_Bins.GetUpperBound(0))
{
if (x != 0)
{
iSize = m_Items[i].size;
for (j = 0; j < m_Bins.GetUpperBound(0); j++)
{
if (m_Bins[j] + iSize <= m_BinCapacity)
{
m_Bins[j] = m_Bins[j] + iSize;
m_Bins[m_Bins.GetUpperBound(0)] = m_Bins[m_Bins.GetUpperBound(0)] - iSize;
m_Items[i].lBin = j;
Debug.Print("moved an item out of last bin");
//leave if only the first item remains in last bin
if (m_Bins[m_Bins.GetUpperBound(0)] == x)
{
//INSTANT C# WARNING: Exit statements not matching the immediately enclosing block are converted using a 'goto' statement:
//ORIGINAL LINE: Exit Do
goto ExitLabel1;
}
break;
}
}
}
else
{
x = m_Items[i].size; //flag that we found and skipped first (largest) item in last bin
}
}
// If j = UBound(m_Bins) Then Exit For
i = i + 1;
} while (i <= m_Items.GetUpperBound(0)); //Next
ExitLabel1:
// SortPackagesByBin 'let user call this so we can see how binsort was executed
}
//This is automatically trnaslated from VB code and definitely needs substantial editing to work
//translated using www.tangiblesoftwaresolutions.com
#include <string>
class modCBinPackage final
{
public:
class tPackage
{
public:
int size = 0;
int lBin = 0; //bin where it has been placed
std::wstring name; //optional for caller's use (e.g. filename)
};
};
//another module
private:
//VB TO C++ CONVERTER WARNING: VB to C++ Converter has converted this array to a pointer. You will need to call 'delete[]' where appropriate:
//ORIGINAL LINE: Private m_Items() As tPackage //New cBinPackage
tPackage **m_Items; //New cBinPackage
//VB TO C++ CONVERTER WARNING: VB to C++ Converter has converted this array to a pointer. You will need to call 'delete[]' where appropriate:
//ORIGINAL LINE: Private m_Bins() As Integer //used space
int *m_Bins; //used space
int m_BinCapacity = 0;
int m_BinReasonablyFull = 0; //threshold that tells whether to use BestFit or WorstFit
int m_iUItem = 0; //when adding packages array may be larger than necessary
//this keeps track of the last item before BinPacking
//array is shrunk so that ubound is valid
public:
void PackBins()
{
int j = 0;
int i = 0;
int tot = 0;
int qWorstBin = 0;
int iWorstBin = 0;
int iBestBin = 0;
int qBestBin = 0;
int x = 0;
int iSize = 0; //=m_Items(i).Size
int prevUbound = 0;
pTightenPackageList();
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
if (m_Items->GetUpperBound(0) == 0) //1 item
{
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to resize an array:
ReDim m_Bins[m_iUItem]; //so BinsNeeded will give correct val
return;
}
if (m_BinReasonablyFull == 0)
{
m_BinReasonablyFull = static_cast<int>(0.95 * m_BinCapacity);
}
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
for (i = 0; i <= m_Items->GetUpperBound(0); i++)
{
if (m_Items[i]->size <= m_BinCapacity)
{
tot = tot + m_Items[i]->size;
}
}
//start with one less than min bins necessary to hold all items
//when remainder of tot / m_BinCapacity < 0.5
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to resize an array:
ReDim m_Bins[static_cast<int>(floor(static_cast<double>(tot / static_cast<double>(m_BinCapacity)))) + static_cast<int>((tot % m_BinCapacity) < m_BinCapacity / 2.0)];
//place all items over 1/2 capacity in their own bin
qBestBin = static_cast<int>(floor(static_cast<double>(m_BinCapacity / 2.0)));
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
for (i = 0; i <= m_Items->GetUpperBound(0); i++)
{
iSize = m_Items[i]->size;
if (iSize > qBestBin)
{
if (iSize <= m_BinCapacity)
{
m_Items[i]->lBin = i;
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
if (i > m_Bins->GetUpperBound(0))
{
pNewBin();
}
m_Bins[i] = iSize; //mark bin usage
}
else
{
m_Items[i]->lBin = -1; //oversized
}
}
else
{
break; // <= 1/2 bin capacity
}
}
//place the rest of the items
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
for (i = i; i <= m_Items->GetUpperBound(0); i++)
{
//loop until a bin has been found
m_Items[i]->lBin = -1; //no bin chosen yet
// If m_Items(i).size <= m_BinCapacity Then NOT NEEDED NOW THAT WE PREPLACE LARGE ITEMS
iBestBin = -1; //best bin index and flag that best bin found
iWorstBin = -1; //worst bin index and flag that fits in bin
qBestBin = m_BinReasonablyFull - 1; //a best bin has to be > this
qWorstBin = m_BinCapacity + 1;
iSize = m_Items[i]->size;
j = 0; //current bin to check
do
{
x = m_Bins[j] + iSize;
//if fits in bin
if (x <= m_BinCapacity)
{
//is it most full bin
if (x > qBestBin) //NOW qBestBin always= m_BinReasonablyFull-1
{
//This saves 10% time and produced no difference in bins needed
//for 600,000 reps with 100 random items
// If x = m_BinCapacity Then 'no need to check for better fit
//this is actually very common for small items when
//dealing with thousands of items
m_Items[i]->lBin = j;
m_Bins[j] = x; // m_Bins(j) + iSize
break;
}
//is it least full bin
if (x < qWorstBin)
{
qWorstBin = x;
iWorstBin = j;
}
}
//if current bin is empty or last bin and don't need new one it's time to decide where to place item
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
if ((m_Bins[j] == 0) || (j == m_Bins->GetUpperBound(0)))
{
if (iWorstBin >= 0)
{
m_Items[i]->lBin = iWorstBin;
m_Bins[iWorstBin] = m_Bins[iWorstBin] + iSize;
break;
}
else //didn't fit - place in the empty bin or in new bin
{
if (m_Bins[j] != 0)
{
//we need a new bin (rare since we start with min bins
pNewBin();
j = j + 1;
}
m_Items[i]->lBin = j;
m_Bins[j] = m_Bins[j] + iSize;
break;
}
}
//try next bin
j = j + 1;
} while (true); //While m_Items(i).lBin = -1 'now exit do takes care 15%faster in IDE
// End If 'oversized package test
}
//--------------------------------------------------------------
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
if (m_Bins[m_Bins->GetUpperBound(0)] == 0 && m_Bins->GetUpperBound(0) > 0)
{
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to resize an array:
ReDim Preserve m_Bins[m_Bins->GetUpperBound(0) - 1];
}
//try and place last items as 1st fit
//keep last bin as empty as possible
x = 0; //: j = 0
i = 0;
do //For i = 0 To UBound(m_Items)
{
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
if (m_Items[i]->lBin == m_Bins->GetUpperBound(0))
{
if (x != 0)
{
iSize = m_Items[i]->size;
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
for (j = 0; j < m_Bins->GetUpperBound(0); j++)
{
if (m_Bins[j] + iSize <= m_BinCapacity)
{
m_Bins[j] = m_Bins[j] + iSize;
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
m_Bins[m_Bins->GetUpperBound(0)] = m_Bins[m_Bins->GetUpperBound(0)] - iSize;
m_Items[i]->lBin = j;
Debug::Print(L"moved an item out of last bin");
//leave if only the first item remains in last bin
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
if (m_Bins[m_Bins->GetUpperBound(0)] == x)
{
//VB TO C++ CONVERTER WARNING: Exit statements not matching the immediately enclosing block are converted using a 'goto' statement:
//ORIGINAL LINE: Exit Do
goto ExitLabel1;
}
break;
}
}
}
else
{
x = m_Items[i]->size; //flag that we found and skipped first (largest) item in last bin
}
}
// If j = UBound(m_Bins) Then Exit For
i = i + 1;
//VB TO C++ CONVERTER TODO TASK: Native C++ has no direct way to determine the length or upper bound of a specific dimension of an array:
} while (i <= m_Items->GetUpperBound(0)); //Next
ExitLabel1: ;
// SortPackagesByBin 'let user call this so we can see how binsort was executed
}
